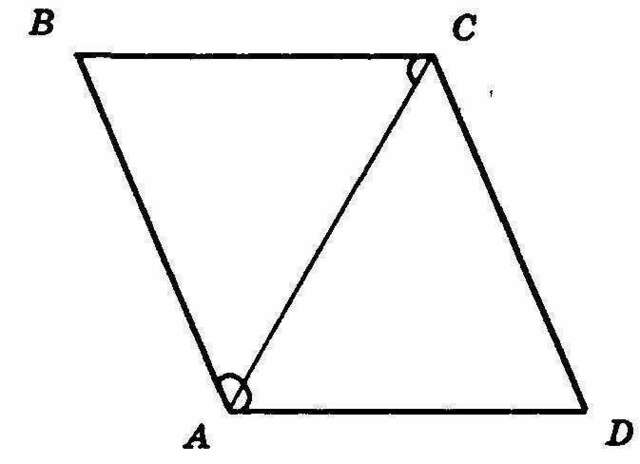
Смотри вложение.
Пусть АС биссектриса и диагональ в параллелограмме ABCD
тогда
(как накрест лежащие углы для параллельных ВС и AD и секущей АС). Тогда,
а значит треугольник ABC
равнобедренный с основанием AC
Значит, AB=BC
По свойству параллелограмма
AB=CD,BC=AD
как противоположные стороны. Итак, все стороны параллелограмма ABCD равны, значит, он ромб. Что и требовалось доказать.